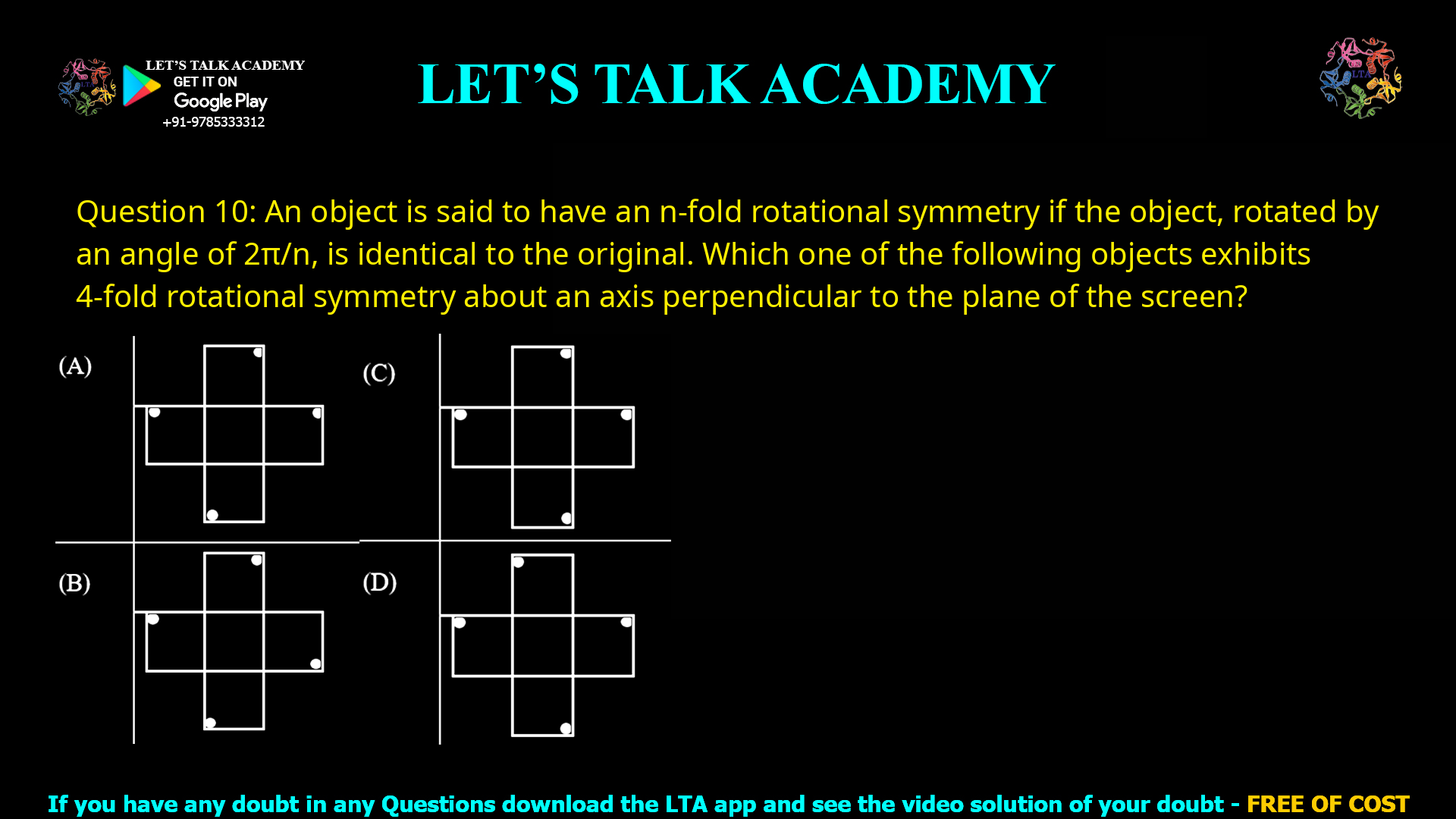
Q.10 An object is said to have an n-fold rotational symmetry if the object, rotated by an angle of 2π/n, is identical to the original.
Which one of the following objects exhibits 4-fold rotational symmetry about an axis perpendicular to the plane of the screen?
Note: The figures shown are representative.
Introduction
Rotational symmetry is an important concept in physics and geometry, especially in questions related to symmetry operations. An object is said to possess n-fold rotational symmetry if rotating it by an angle of 360°/n results in an appearance identical to the original.
In this article, we analyze a multiple-choice question asking which object exhibits 4-fold rotational symmetry about an axis perpendicular to the plane of the screen, and we explain why only one option is correct.
Understanding 4-Fold Rotational Symmetry
An object has 4-fold rotational symmetry if it looks exactly the same after rotations of:
-
90°
-
180°
-
270°
-
360°
This means the object repeats itself four times during one full rotation.
Correct Answer
✅ Correct Option: (C)
Explanation of Each Option
Option (A): ❌ Incorrect
-
Although the shape resembles a cross, the positions of the black dots are not symmetric under a 90° rotation.
-
After rotation, the dots shift to different relative positions.
-
The object may show 2-fold symmetry, but not 4-fold symmetry.
👉 Fails the 90° rotation test
Option (B): ❌ Incorrect
-
The arms of the shape are unequal in dot placement.
-
Rotating the figure by 90° does not reproduce the original configuration.
-
Symmetry breaks due to asymmetric dot distribution.
👉 Not invariant under quarter-turn rotation
Option (C): ✅ Correct
-
The object is perfectly symmetric in shape and dot placement.
-
Rotating it by 90°, 180°, or 270° gives the same appearance.
-
All four arms are identical and equally spaced.
👉 Satisfies the definition of 4-fold rotational symmetry
Option (D): ❌ Incorrect
-
The vertical and horizontal arms are not equivalent.
-
Dot placement is asymmetric across different directions.
-
Only 180° rotation preserves similarity.
👉 Exhibits 2-fold symmetry, not 4-fold
Why Option (C) Is the Only Correct Choice
| Rotation Angle | Appearance Matches Original? |
|---|---|
| 90° | ✅ Yes |
| 180° | ✅ Yes |
| 270° | ✅ Yes |
| 360° | ✅ Yes |
Only Option (C) remains unchanged under all required rotations.
Key Takeaway
-
4-fold rotational symmetry requires perfect repetition every 90°.
-
Both shape and internal features (like dots) must align after rotation.
-
Option (C) uniquely satisfies this condition.
Conclusion
Understanding rotational symmetry helps solve a wide range of physics and geometry problems efficiently. By carefully checking symmetry under rotation angles, we can confidently conclude that Option (C) is the correct answer for this question.
📌 Final Answer: Option (C)